Privacy
In Part 1 we covered why privacy is essential for widespread cryptocurrency adoption, and concluded that neither Bitcoin nor Ethereum, or even ZCash is suitable for the task we’re wanting to solve: anonymity with efficiency. (Also the bonus property of needing no trusted setup)!
COOL THING 1: STEALTH ADDRESSES
The benefits of using stealth addresses can be explained through this slightly contrived example:
Say Alice has a store, and she has her public key stuck to her till, so people can make payments to her in bitcoin/ethereum/ZCash. Alice is aware of the transaction analysis that people can perform on public blockchains, and her competitor Eve knows that about 98% of store payments are in Ether, so if she tracks Alice’s blockchain address, she will be able to monitor how Alice’s business is doing in near-real time. This makes Alice’s business vulnerable. For example, Eve could even learn to predict when Alice runs out of stock and then sell items to Alice at an unfair price. Instead of Alice changing her public key sticker every day, she can use stealth addresses!
Stealth addresses work as follows:
Say Alice has long-term, publicly known public key , and corresponding private key
, such that
, with
the generator of an elliptic curve (EC) group (if you don’t know what that means, we can just pretend they’re coordinates plotted on a graph with the property that
is an excessively obscure representation which does not reveal the secret
).
is an elliptic curve point (as is
— it’s defined along with the curve we’re working on) and
is a 256 bit integer.
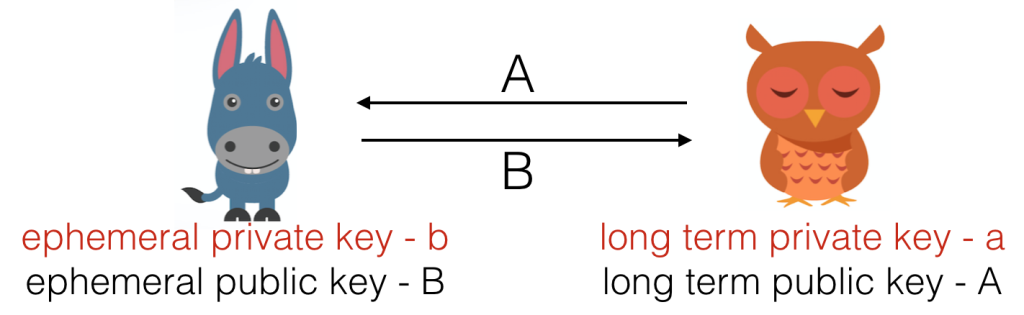
Bob wants to pay Alice. Normally he would just send Ether to Alice, but as we know, blockchain analysis would make this transaction entirely public. So instead, Bob’s wallet generates an ephemeral key pair, for use in just this one transaction, with an elliptic curve point, and
a 256 bit integer. Bob (or Bob’s wallet, acting on his behalf) sends
to Alice, and they can both calculate the shared secret
.

Bob can then send the Ether to an address formed ) (…with
being the function used to map from public keys to public addresses in Ethereum), and Alice can spend the money with private key
.
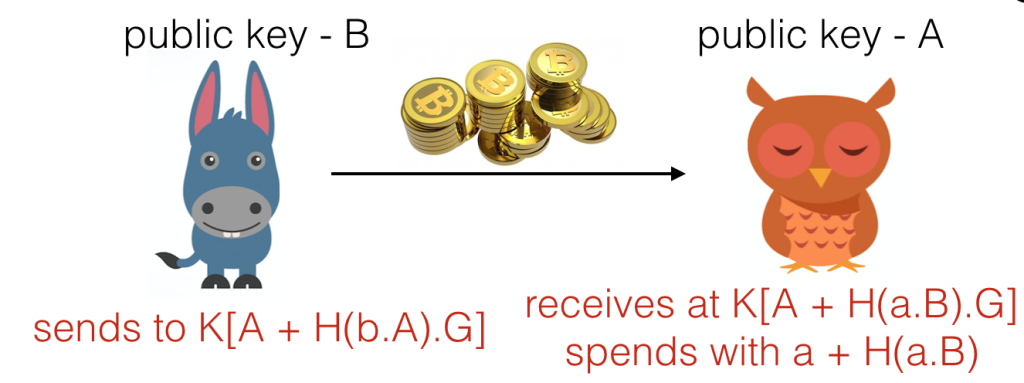
For any eavesdropper to compute the shared secret , they would have to crack the ECDH (elliptic curve Diffie-Hellman) problem. This is infeasible. So Alice’s privacy is protected so far!!
While we’re here, here are the definitions of ECDLP & EC-DDH. Both are useful in different parts of our huge scheme. The assumed hardness of the ECDLP is essential for privacy in the stealth address system, and the hardness of EC-DDH is the requirement for our ring signature scheme, described in Part 3. Assume E here is for Eve, our adversary (conventionally, the adversary is called A for adversary, but we have as Alice’s public key, so we can call the adversary E to avoid confusion between E, the malicious actor, and
, the elliptic curve point).
Definition 1 Elliptic Curve Discrete Logarithm Problem (ECDHP)
E has no advantage in solving following:
Given and
,
find .
Definition 2 Decisional Diffie-Hellman Assumption (EC-DDH)
E has no advantage in the following:
Given , with
, decide whether
.
Although the maths may look somewhat difficult to follow, Bob can send his one-time-use public key in the ‘data’ slot of the transaction, and so Alice can simply scan all transactions, find B, form the stealth private key, and spend the money as she wishes. The extra computations can all be automating inside and Alice and Bob’s wallets, and the communication is compressed down into 1 transaction needed, just like an entirely transparent result. This functionality is entirely possible with Ethereum & any wallet with stealth address capabilities.
However, if Eve is transferring money to Alice, and is really invested in finding out Alice’s income, she could produce a transaction (or many dust transactions) with stealth addresses for Alice, and then monitor the blockchain to see if Alice ever joins those accounts together or with others, in order to make an input to a higher value transaction in the future. This sounds unlikely to be relevant, but blockchain analysis (such as taint analysis) has been known to have crippling effects on the anonymity of public blockchain systems.
So we will work to prevent it. Using cool thing number 2.
Pingback: Blockchain Privacy – Part 1: Blockchains & Why We Need Privacy | Financial Cryptography, Bitcoin, Crypto Currencies, Cryptanalysis
Pingback: Blockchains and Why We Need Privacy – Bentham’s Gaze